And, it's the last day of ramadhan!
*uraaa
Well, tomorow, there will be many foods here, in my house, and when i'm bored with the food here
I can go to my neighbour or other family member house, and eat!
And, there is a possibility to be a rich person tomorow
Ok, it's a little bit loud right here, and when i ask one of my friend, she said, it's loud too there
the sounds of firework, firecracker, and other stuff (Including takbir) are here, i'm afraid that one of of that sounds around me is a military class explosion (?)
Well, if you want some kind of artilery battle feeling, you can wait till' the new year, and come to the nearest firework party, but , dont get too close, get a little bit far (500m maybe work), and look for a quiet place, wait till 00.00, and feel it
Ok, i'm talking too much shit now
I need to continue my kerbal space program rocket
Well, if you think, kerbal space program is only an ordinary game, i'll proof you are wrong
I will tell you how to orbit
First, you need to adjust your orbiting speed
The relation between orbital speed and acceleration is given by the formula:

where a is the acceleration due to gravity, v is the horizontal speed, and r is the radius of orbit.
Of course, gravity varies depending on your distance from the planet, so we also need the following formula to determine a based on your altitude:

where g is the acceleration due to gravity at sea level (9.807 m/s2), R is the radius of Kerbin (600 km), and h is the altitude of your orbit.
Note: Since the radius of your orbit r is equal to the radius of Kerbin R plus your altitude h, we can substitute R + h for r.
Now we have two expressions for a, so we set them on opposite sides of an equation and simplify:
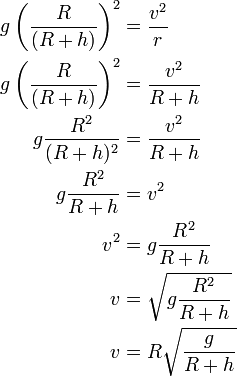
Finally, substituting known values for g and R,
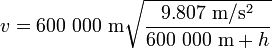
And then, the orbital period
From the basic mechanics formula:

We know v from the above, and d is simply the circumference of a circle with a radius equal to your orbital altitude plus the radius of Kerbin:

And, last but not least, orbital equation
For this section it is assumed that the craft in question is orbiting a particular body and is a lot smaller than the body that it is orbiting. Other then in the general orbital equation and the energy equation, the orbits are assumed to be bounded orbits completely within the body's sphere of influence and no others. This section also assumes that classical physics applies in the game. All distances and radii are from the center of the body being orbited and the sea level radius of the body needs to be added to the altitude given in game to recover the values here. The section uses the standard gravitational parameter
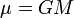 which
which 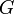 is Newton's Gravitational Constant and
is Newton's Gravitational Constant and 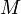 is the mass of the body that is being orbited. From here on out
is the mass of the body that is being orbited. From here on out  will refer to the mass of the craft.
will refer to the mass of the craft.
When the craft is orbiting a body, the distance between the craft and the body is given by the equation
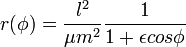
where
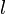 is the angular momentum of the craft,
is the angular momentum of the craft,  is the eccentricity of the orbit, and
is the eccentricity of the orbit, and 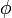 is an angle parameter for the orbit.
is an angle parameter for the orbit. 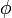 runs from
runs from 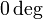 to
to 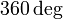 ,
, 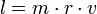 at apoapsis or periapsis, and
at apoapsis or periapsis, and 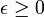 . When
. When 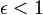 the orbit is bounded and is an ellipse and when
the orbit is bounded and is an ellipse and when 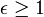 the orbit is unbounded. At
the orbit is unbounded. At  the craft is at the periapsis and at
the craft is at the periapsis and at  the craft is at the apoapsis. At periapsis,
the craft is at the apoapsis. At periapsis,
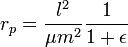
and at apoapsis,
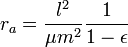 .
.
The semimajor axis is
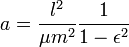
and the semiminor axis is
 .
.
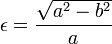
Given the results for
 and
and 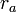 above,
above,
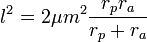 and
and
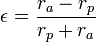 thus
thus
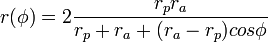
The velocity for an object in elliptical orbit about a much larger object is
 .
.
The energy for an object in orbit is
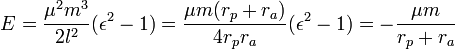 .
.
One should note that for bounded orbits, the energy is negative and for escape orbits, energy is non-negative.
The orbital period is
 .
.
Let
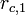 and
and 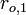 be the two apsides of a given orbit and let a craft execute a burn imparting a specific
be the two apsides of a given orbit and let a craft execute a burn imparting a specific  all at the single point in time the craft is at
all at the single point in time the craft is at 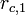 . For this problem
. For this problem  can be either positive or negative. If it is positive then the thrust
is to speed up the craft but if it is negative the ture delta v is the
oppositie of that in the problem but the thrust is to slow down the
craft. This problem assumes that the thust is in the same or opposite
direction of travel and is not enough to reverse the craft. The new
orbit will have apsides of
can be either positive or negative. If it is positive then the thrust
is to speed up the craft but if it is negative the ture delta v is the
oppositie of that in the problem but the thrust is to slow down the
craft. This problem assumes that the thust is in the same or opposite
direction of travel and is not enough to reverse the craft. The new
orbit will have apsides of 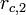 and
and 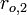 with
with  .
.
The speed of the craft before the burn is
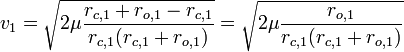 .
.
The speed of the craft after the burn is
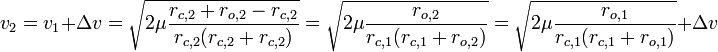
which yields
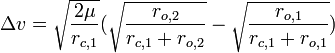
and
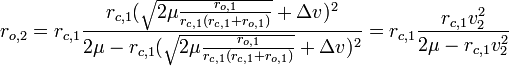
Well, still thinking that game give you nothing?
Think again
Well, i want to go now
continue build some rocket
Bye!
xoxo (well, is there anyone know why "xoxo" means hug and kiss?)
Ps. Again, Ied Mubarak All!
Tidak ada komentar:
Posting Komentar